Dimewiki

Difference between revisions of "Power Calculations in Stata"

Jump to: navigation, search
 
(16 intermediate revisions by 5 users not shown)
Line 1: Line 1:
<span style="font-size:150%">
[[Sample Size and Power Calculations| Power calculations]] indicate the minimum sample size needed to provide precise estimates of the program impact; they can also be used to compute power and [[Minimum Detectable Effect | minimum detectable effect size]]. Researchers should conduct power calculations during research design to determine sample size, power, and/or MDES, all of which play critical roles in informing [[Preparing for Field Data Collection | data collection planning]], [[Survey Budget|budget]], timeline, accuracy, and precision.
<span style="color:#ff0000"> '''NOTE: this article is only a template. Please add content!''' </span>
This page presents different options of Stata commands for power calculations and discusses the advantages and disadvantages associated with each.
</span>
==Read First==
*[[Power Calculations in Optimal Design|Optimal Design]] provides helpful visualizations for power calculations that may aid understanding of power calculations in Stata.
*[http://www.stata.com/ Stata] is better than Optimal Design for [[Reproducible Research|reproducible research]] purposes, as the power calculations are codified in a do file. 
*To install the commands covered in this page, search <code>findit</code>, followed by the command name. Then find the most recent update of the command and install it. For more information on each command, type <code>help</code>, followed by the command name. Note that <code>power</code> is Stata’s built-in program for sample size calculations and does not need to be installed.
*For more information on the key parameters of power calculations, see [[Sample Size and Power Calculations]].
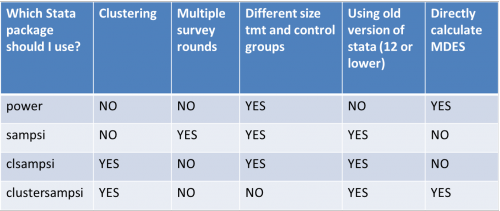
*The below table outlines the capabilities of four Stata commands for power calculations. More detailed descriptions follow.
[[File:Power_Calcs_in_Stata_Quick_Reference.png|500px]]


==power==
<code>power</code> is a built-in program and Stata’s newest update to power calculations. It was introduced with Stata13 as a replacement to <code>sampsi</code>. It is best used for simple randomizations with no clustering.
===Advantages===
* Offers more flexibility of input/output choices
* Generates better outputs including more information and a graph option
* Automatically saves output to a file
* Can compute the [[Sample Size | sample size]] of control group given a treatment group size (or vice versa)
* Directly calculates [[Minimum Detectable Effect | MDES]]
===Disadvantages===
* No straightforward way to control for repeated measures
* Allows for treatment and control groups of different sizes


add introductory 1-2 sentences here
===Useful Options===
 
* <code>power onemean</code>: assumes equal means in treatment and control
 
*Sample size
 
** <code>n()</code>: sample size
== Read First ==
** <code>n1()</code>: control group size
* include here key points you want to make sure all readers understand
**<code>n2()</code>: treatment group size
 
** <code>nratio</code>: ratio of n1/n2. Its default is 1. It is not necessary to specify this if you specify <code>n1</code> and <code>n2</code>
 
* <code>table</code> outputs results in a table format
== Guidelines ==
* <code>saving(filename, [replace])</code> saves results in a .dta format
 
=== What data do I need? ===
 
You must have:  
* Mean and variance for outcome variable for your population 
** Typically can assume mean and SD are the same for treatment and control groups if randomized
 
* Sample size (assuming you are calculating MDES (δ))
** If individual randomization, number of people/units (n)
** If clustered, number of clusters (k), number of units per cluster (m), intracluster correlation (ICC, ρ) and ideally, variation of cluster size
 
* The following standard conventions
** Significance level (α) = 0.05
** Power = 0.80 (i.e. probability of type II error (β) = 0.20
 
 
Ideally, you will also have:
* Baseline correlation of outcome with covariates
** Covariates (individual and/or cluster level) reduce the residual variance of the outcome variable, leading to lower required sample sizes
*** Reducing individual level residual variance is akin to increasing # obs per cluster (bigger effect if ICC low)
*** Reducing cluster level residual variance is akin to increasing # of clusters (bigger effect if ICC and m high)
**If you have baseline data, this is easy to obtain
*** Including baseline autocorrelation will improve power (keep only time invariant portion of variance)
 
* Number of follow-up surveys
 
* Autocorrelation of outcome between FUP rounds
 
=== How do I get this data? ===
 
You will basically never have the data you need for your exact population of interest at the time when you first do power calculations.
 
You will need to use the best available data to estimate values for each parameter. Sources to consider:
* High-quality nationally representative survey (e.g. LSMS)
* Data from DIME IE in same country (or region, if pressed)
* Review the literature – especially published papers on the sector and country. What kind of effects? Summary stats available?
 
If you can’t come up with a specific value you feel very confident in, run a few different power calculations with alternate assumptions and create bounded estimates.  
 
=== Stata Command Options ===


Quick Reference on options:
==sampsi==
<code>sampsi</code> is no longer an officially supported Stata package. It has been replaced by <code>power</code>. However, it continues to work. By default, the command computes sample size. To compute power, specify <code>n1</code> or <code>n2</code>. To compare means (not proportions), specify <code>sd1()</code> or <code>sd2()</code>. For repeated measures, <code>sd1()</code> or <code>sd2()</code> must be specified. Note that <code>sampsi</code> defaults to 90% power.


[[File:Power_Calcs_in_Stata_Quick_Reference.png|500px]]
===Advantages===
* Works with Stata13 or earlier
* Allows repeated measures (multiple follow-ups)
===Disadvantages===
* Does not allow clustering
* Requires user to impute MDES
===Useful Options===
*<code>onesample</code>: assumes equal means in treatment and control
* Sample size
** <code>n1()</code>: size of treatment group
** <code>n2()</code>: size of control group
** <code>ratio()</code>: n1/n2, default is 1
* Repeated measures
** <code>pre</code>: number of baseline measurements
** <code>post</code>: number of follow-up measurements
** <code>r0()</code>: correlation between baseline measures (default r0 = r1)
** <code>r1()</code>: correlation between follow-up measures
** <code>r01()</code>: correlation between baseline and follow-up
* <code>method()</code>: options include <code>post</code>, <code>change</code>,  <code>anova</code>, or <code>all</code>. The default is <code>all</code>.
*<code>sampclus</code> is an add-on to <code>sampsi</code> that allows for clustering. It must be directly preceded by <code>sampsi</code> command. For example, the following code correct sample size and computes the number of clusters from a t-test. It then adjusts this sample size calculation for 10 observations per cluster and an ICC of 0.2:
<nowiki>
sampsi 200 185, alpha(.01) power(.8) sd(30)
sampclus, obsclus(10) rho(.2)</nowiki>
===Computing MDES with <code>sampsi</code>===
To compute MDES with <code>sampsi</code>, use a guess-and-check method. The difference between baseline and hypothesized mean is MDES. Compute power, using different hypothesized means, aiming for power = 0.8.


==clsampsi==
===Advantages===
* Allows for clustering
===Disadvantages===
* Requires user to impute MDES
* Does not allow for repeated measures
* Does not allow for baseline correlation
===Useful options===
* <code>m()</code>: cluster size in treatment and control, assuming equal cluster size in each group. If the treatment and control cluster sizes differ, use <code>m1()</code> and <code>m2()</code> for the control and treatment cluster sizes, respectively.
* <code>k()</code>: number of clusters in treatment and control, assuming equal number of clusters in each group. If the number of clusters differs between treatment and control, use <code>k1()</code> and <code>k2()</code> for the control and treatment cluster numbers, respectively.
* <code>sd()</code>: standard deviation, assuming it is equal between the treatment and control groups. If the treatment and control standard deviation differs, use <code>sd1()</code> and <code>sd2(#)</code> for the control and treatment standard deviations, respectively.
* <code>rho(#)</code>: ICC assuming it is equal between the treatment and control groups. Alternatively, use <code>rho1()</code> and <code>rho2()</code>.
* <code>sampsi</code> determines the power of means (or proportion) comparison using the standard <code>sampsi</code> command
* <code>varm(#)</code>: cluster size variation, assuming it is the same between the treatment and control groups. This only affects the power if it is larger than <code>m()</code> and <code>rho()</code>>0.


==== ''power'' ====
==clustersampsi==
Stata’s newest updated to power calculations. Introduced with Stata13, replaces ''sampsi''.
===Advantages===
 
* Allows for clustering
Pros
* Allows for baseline correlations
* More flexible in terms of input/output choices
* Directly calculates MDES
* Better output: more info, graph option
===Disadvantages===
* Automatically saves output to a file
* Doesn’t allow for different sized treatment / control groups
* Can compute sample size of control group given treatment group size (or vice versa)
* Doesn’t allow for repeated measures
* Directly calculate MDES
===Useful options===
 
* <code>detectabledifference</code> calculates MDES
Cons
** Alternative options: <code>power</code>, <code>samplesize</code>
* Doesn’t allow for clustering
** to use detectable difference, specify <code>m</code>, <code>k</code>, <code>mu1</code>
* No straightforward way to control for repeated measures
* <code>rho()</code>: ICC
* Allows for treatment and control groups of different sizes
* <code>k()</code>: number of clusters in each arm
 
* <code>m()</code> average cluster size
==== ''sampsi'' ====
* <code>size_cv()</code>: coefficient of variation of cluster sizes (default is 0). Can be any number greater than 1.
==== ''clsampsi'' ====
* <code>mu1()</code> and <code>mu2()</code>: mean for treatment and control, respectively
==== ''clustersampsi'' ====
* <code>sd1()</code> and <code>sd2()</code>: mean for treatment and control, respectively
==== ''rdpower'' ====
* <code>base_correl</code> correlation between baseline measurements – or other predictive covariates – and outcome


== Back to Parent ==
== Back to Parent ==
This article is part of the topic [[Sampling & Power Calculations]]
This article is part of the topic [[Sampling & Power Calculations]]


== Additional Resources ==
== Additional Resources ==
* list here other articles related to this topic, with a brief description and link
*DIME Analytics guidelines on survey sampling and power calculations [https://github.com/worldbank/DIME-Resources/blob/master/survey-sampling-1.pdf 1] and [https://github.com/worldbank/DIME-Resources/blob/master/survey-sampling-2.pdf 2]
*Batistatou et al.’s [https://www.stata-journal.com/sjpdf.html?articlenum=st0329 Sample size and power calculations for trials and quasi-experimental studies with clustering], which focuses on applications of <code>clsampsi</code>
*Bharti’s [https://www.stata.com/meeting/india13/materials/in13_bharti_s.pdf Standalone use of STATA for analysis of cluster randomized controlled trials]
* Berk Ozler’s [http://blogs.worldbank.org/impactevaluations/power-calculations-what-software-should-i-use Power Calculations: What software should I use?] via the Development Impact blog
* Andrew Gelman’s [http://andrewgelman.com/2017/03/03/yes-makes-sense-design-analysis-power-calculations-data-collected/ Why it makes sense to revisit power calculations after data has been collected]
*JPAL’s [https://www.povertyactionlab.org/sites/default/files/resources/2017.01.11-The-Danger-of-Underpowered-Evaluations.pdf The Danger of Underpowered Evaluations]


[[Category: Sampling & Power Calculations]]
[[Category: Sampling & Power Calculations]]
[[Category: Reproducible Research]]

Latest revision as of 14:20, 13 April 2021

Power calculations indicate the minimum sample size needed to provide precise estimates of the program impact; they can also be used to compute power and minimum detectable effect size. Researchers should conduct power calculations during research design to determine sample size, power, and/or MDES, all of which play critical roles in informing data collection planning, budget, timeline, accuracy, and precision. This page presents different options of Stata commands for power calculations and discusses the advantages and disadvantages associated with each.

Read First

  • Optimal Design provides helpful visualizations for power calculations that may aid understanding of power calculations in Stata.
  • Stata is better than Optimal Design for reproducible research purposes, as the power calculations are codified in a do file.
  • To install the commands covered in this page, search findit, followed by the command name. Then find the most recent update of the command and install it. For more information on each command, type help, followed by the command name. Note that power is Stata’s built-in program for sample size calculations and does not need to be installed.
  • For more information on the key parameters of power calculations, see Sample Size and Power Calculations.
  • The below table outlines the capabilities of four Stata commands for power calculations. More detailed descriptions follow.

Power Calcs in Stata Quick Reference.png

power

power is a built-in program and Stata’s newest update to power calculations. It was introduced with Stata13 as a replacement to sampsi. It is best used for simple randomizations with no clustering.

Advantages

  • Offers more flexibility of input/output choices
  • Generates better outputs including more information and a graph option
  • Automatically saves output to a file
  • Can compute the sample size of control group given a treatment group size (or vice versa)
  • Directly calculates MDES

Disadvantages

  • No straightforward way to control for repeated measures
  • Allows for treatment and control groups of different sizes

Useful Options

  • power onemean: assumes equal means in treatment and control
  • Sample size
    • n(): sample size
    • n1(): control group size
    • n2(): treatment group size
    • nratio: ratio of n1/n2. Its default is 1. It is not necessary to specify this if you specify n1 and n2
  • table outputs results in a table format
  • saving(filename, [replace]) saves results in a .dta format

sampsi

sampsi is no longer an officially supported Stata package. It has been replaced by power. However, it continues to work. By default, the command computes sample size. To compute power, specify n1 or n2. To compare means (not proportions), specify sd1() or sd2(). For repeated measures, sd1() or sd2() must be specified. Note that sampsi defaults to 90% power.

Advantages

  • Works with Stata13 or earlier
  • Allows repeated measures (multiple follow-ups)

Disadvantages

  • Does not allow clustering
  • Requires user to impute MDES

Useful Options

  • onesample: assumes equal means in treatment and control
  • Sample size
    • n1(): size of treatment group
    • n2(): size of control group
    • ratio(): n1/n2, default is 1
  • Repeated measures
    • pre: number of baseline measurements
    • post: number of follow-up measurements
    • r0(): correlation between baseline measures (default r0 = r1)
    • r1(): correlation between follow-up measures
    • r01(): correlation between baseline and follow-up
  • method(): options include post, change, anova, or all. The default is all.
  • sampclus is an add-on to sampsi that allows for clustering. It must be directly preceded by sampsi command. For example, the following code correct sample size and computes the number of clusters from a t-test. It then adjusts this sample size calculation for 10 observations per cluster and an ICC of 0.2:
sampsi 200 185, alpha(.01) power(.8) sd(30)
sampclus, obsclus(10) rho(.2)

Computing MDES with sampsi

To compute MDES with sampsi, use a guess-and-check method. The difference between baseline and hypothesized mean is MDES. Compute power, using different hypothesized means, aiming for power = 0.8.

clsampsi

Advantages

  • Allows for clustering

Disadvantages

  • Requires user to impute MDES
  • Does not allow for repeated measures
  • Does not allow for baseline correlation

Useful options

  • m(): cluster size in treatment and control, assuming equal cluster size in each group. If the treatment and control cluster sizes differ, use m1() and m2() for the control and treatment cluster sizes, respectively.
  • k(): number of clusters in treatment and control, assuming equal number of clusters in each group. If the number of clusters differs between treatment and control, use k1() and k2() for the control and treatment cluster numbers, respectively.
  • sd(): standard deviation, assuming it is equal between the treatment and control groups. If the treatment and control standard deviation differs, use sd1() and sd2(#) for the control and treatment standard deviations, respectively.
  • rho(#): ICC assuming it is equal between the treatment and control groups. Alternatively, use rho1() and rho2().
  • sampsi determines the power of means (or proportion) comparison using the standard sampsi command
  • varm(#): cluster size variation, assuming it is the same between the treatment and control groups. This only affects the power if it is larger than m() and rho()>0.

clustersampsi

Advantages

  • Allows for clustering
  • Allows for baseline correlations
  • Directly calculates MDES

Disadvantages

  • Doesn’t allow for different sized treatment / control groups
  • Doesn’t allow for repeated measures

Useful options

  • detectabledifference calculates MDES
    • Alternative options: power, samplesize
    • to use detectable difference, specify m, k, mu1
  • rho(): ICC
  • k(): number of clusters in each arm
  • m() average cluster size
  • size_cv(): coefficient of variation of cluster sizes (default is 0). Can be any number greater than 1.
  • mu1() and mu2(): mean for treatment and control, respectively
  • sd1() and sd2(): mean for treatment and control, respectively
  • base_correl correlation between baseline measurements – or other predictive covariates – and outcome

Back to Parent

This article is part of the topic Sampling & Power Calculations

Additional Resources

Retrieved from "https://dimewiki.worldbank.org/index.php?title=Power_Calculations_in_Stata&oldid=8124"