Power Calculations in Stata
NOTE: this article is only a template. Please add content!
add introductory 1-2 sentences here
Read First
- include here key points you want to make sure all readers understand
Guidelines
What data do I need?
You must have:
- Mean and variance for outcome variable for your population
- Typically can assume mean and SD are the same for treatment and control groups if randomized
- Sample size (assuming you are calculating MDES (δ))
- If individual randomization, number of people/units (n)
- If clustered, number of clusters (k), number of units per cluster (m), intracluster correlation (ICC, ρ) and ideally, variation of cluster size
- The following standard conventions
- Significance level (α) = 0.05
- Power = 0.80 (i.e. probability of type II error (β) = 0.20
Ideally, you will also have:
- Baseline correlation of outcome with covariates
- Covariates (individual and/or cluster level) reduce the residual variance of the outcome variable, leading to lower required sample sizes
- Reducing individual level residual variance is akin to increasing # obs per cluster (bigger effect if ICC low)
- Reducing cluster level residual variance is akin to increasing # of clusters (bigger effect if ICC and m high)
- If you have baseline data, this is easy to obtain
- Including baseline autocorrelation will improve power (keep only time invariant portion of variance)
- Covariates (individual and/or cluster level) reduce the residual variance of the outcome variable, leading to lower required sample sizes
- Number of follow-up surveys
- Autocorrelation of outcome between FUP rounds
How do I get this data?
You will basically never have the data you need for your exact population of interest at the time when you first do power calculations.
You will need to use the best available data to estimate values for each parameter. Sources to consider:
- High-quality nationally representative survey (e.g. LSMS)
- Data from DIME IE in same country (or region, if pressed)
- Review the literature – especially published papers on the sector and country. What kind of effects? Summary stats available?
If you can’t come up with a specific value you feel very confident in, run a few different power calculations with alternate assumptions and create bounded estimates.
Stata Command Options
Quick Reference on options:
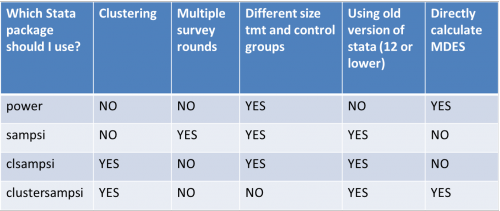
power
Stata’s newest updated to power calculations. Introduced with Stata13, replaces sampsi.
Pros
- More flexible in terms of input/output choices
- Better output: more info, graph option
- Automatically saves output to a file
- Can compute sample size of control group given treatment group size (or vice versa)
- Directly calculate MDES
Cons
- Doesn’t allow for clustering
- No straightforward way to control for repeated measures
- Allows for treatment and control groups of different sizes
When to use? Simple randomizations (no clustering)
Useful options
- power onemean – assume means same in tmt & control
- n sample size
- n1() control group size, n2() treatment group size
- nratio ratio of n1/n2, default is 1 (not necessary to specify if you list n1 and n2)
- power, table outputs results in table format
- power, saving(filename, [replace]) saves results in .dta format
sampsi
No longer an officially supported stata package (replaced by power), though it continues to work. Default is to compute sample size. To compute power: specify n1 or n2. To compare means (not proportions), specify sd1(#) or sd2(#). For repeated measures, sd1(#) or sd2(#) must be specified
Pros
- Works with Stata13 or earlier
- Allows repeated measures (multiple follow-ups)
Cons
- Does not allow clustering
- Have to impute MDES
- Defaults to 90% power (not really a con, but be aware)
Useful Options
- onesample: use if randomized (assume means the same between treatment and control)
- Sample size
- n1(#) size of treatment group
- n2(#) size of control group
- ratio() n1/n2, default is 1
- Repeated measures
- pre number of baseline measurements
- post number of follow-up measurements
- r0(#) correlation between baseline measures (default r0 = r1)
- r1(#) correlation between follow-up measures
- r01(#) correlation between baseline and follow-up
- method(post change anova or all), default is all
How to use sampsi to compute MDES?
- Has to be done through a guess-and-check method. The difference between baseline and hypothesized mean is MDES. Compute power, using different hypothesized means, aiming for power = 0.8.
sampclus is an add-on to sampsi that allows for clustering. It must be directly preceded by sampsi command. For example:
sampsi 200 185, alpha(.01) power(.8) sd(30)
sampclus, obsclus(10) rho(.2)
Corrects sample size and computes number of clusters from a t-test. Adjusts this sample size calculation for 10 observations per cluster and an ICC of 0.2.
clsampsi
Pros
- Allows for clustering
Cons
- Have to impute MDES
- Does not allow for repeated measures
- Does not allow for baseline correlation
Useful options
- m(#) cluster size in treatment and control assuming equal cluster size in tmt & control
- alternative m1(#) and m2(#)
- k(#) number of clusters in tmt and control assuming equal number in tmt & control
- Alternative k1(#) and k2(#)
- sd(#) standard deviation assuming same sd in tmt & control
- Alternative sd1(#) and sd2(#)
- rho(#) ICC assuming same in tmt & control
- Alternatively rho1 and rho2
- sampsi determines power of means (or proportion) comparison using the standard sampsi command
- varm(#) cluster size variation assuming same in tmt & ctl
- only affects power if larger than m(#) and rho(#)>0
clustersampsi
Pros
- Allows for clustering
- Allows for baseline correlations
- Directly calculates MDES
Cons
- Doesn’t allow for different sized treatment / control groups
- Doesn’t allow for repeated measures
Useful options
- detectabledifference calculate MDES
- Alternative options: power, samplesize
- to use detectabledifference must specify m, k, mu1
- rho(#) ICC
- k(#) number of clusters in each arm
- m(#) average cluster size
- size_cv(#) coefficient of variation of cluster sizes (default is 0). Can be any number greater than 1.
- mu1 mean for tmt (mu2 = mean for control)
- sd1 mean for tmt (sd2 = mean for control)
- base_correl correlation btw baseline measurements (or other predictive covariates) and outcome
Back to Parent
This article is part of the topic Sampling & Power Calculations
Additional Resources
- list here other articles related to this topic, with a brief description and link